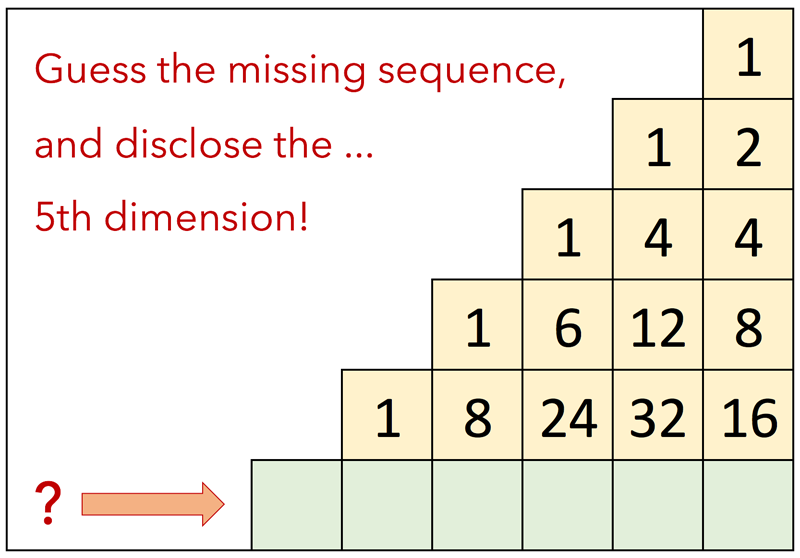
 |
Can you find the missing number sequence?
Don't be misled by the simple linear thinking of other |
Solution: The 5th Dimension
Yeah, it's all about dimensions!Before jumping to the mere formula, let's have a look at what above matrix represents in a multidimensional world.
The first number on top of our matrix (1) represents a dot, a single point with no sizes in a world without dimensions, the whole universe in a dot, a singularity, for some the beginning of our universe itself, but this is a different story. Clone, duplicate our dot and you'll get two dots, connect the dots together and here you have a line lying on a one dimensional space, and that's the second sequence on our matrix (1 - 2), do the same on the third sequence: clone the line, connect the edges and... got it?
Yeah, the third sequence represents a square in a two dimensional space: 4 dots or vertices connected by 4 lines shaping 1 square (1 - 4 - 4). Logically the fourth sequence (1 - 6 - 12 - 8) represents a cube composed by 8 vertices, 12 lines and 6 faces in a three dimensional space.
 |
And now it becomes interesting: using the same analogy, the next sequence would represents a cube in a four dimensional space (a tesseract) and therefore the missing sequence represents a hypercube in the fifth dimension!
Left, a 3D image of a Tesseract shadow while rotating in its own 4th dimension. Yes, we can only visualize its shadow! Fascinating, isnt it? |
The Formula
Each cell in our matrix represents the property (in terms of edges, lines, faces, etc.) of a shape in a given spatial n dimension. And we've seen that a shape in a nth dimensional space is created by cloning/duplicating the corresponding shape in the previous (n - 1) dimension and by connecting all vertices of the two shapes. Take the number 6 in the the 3rd dimension, it represents the six faces of a cube and can be constructed by cloning the corresponding square in the 2nd dimension (1 + 1) and by connecting all edges with 4 lines. At the same way, the 32 lines of our tesseract in the 4th dimension are given by cloning the 12 lines from the shape of the previous dimension (12 + 12) and by adding the corresponding connections (8). So 6 = 2*1 + 4 and 32 = 2*12 + 8.
S(p,n) = 2 * S(p, n-1) + S(p-1 ,n-1)
S = Shape in a cell
p = Property coordinate (column index in our matrix - from right to left)
p = Dimension coordinate (row index in our matrix - from top to bottom)
Or simply: each number in a cell (ie 32) is given by doubling the number in the cell of the previous row (2 * 12) and adding the one from this latter right adjacent cell (8). The missing sequence is then: 1 10 40 80 80 32